
SPSS assumes that the variable that specifies the category is numeric. Selected a cat different from the proportion of people who selected a dog.) (That is, is the proportion of people who
People who selected a cat is different from. Select one of two pets, either a cat or a dog, we could determine if the proportion of Two categories is different from a specified amount.
The binomial test is useful for determining if the proportion of people in one of
#CHISQUARE IN SPSS WINDOWS#
Started SPSS (click on Start | All Programs | SPSS for Windows | SPSS 12.0 for Windows).Downloaded the standard class data set (click on the link and save the data file).
#CHISQUARE IN SPSS HOW TO#
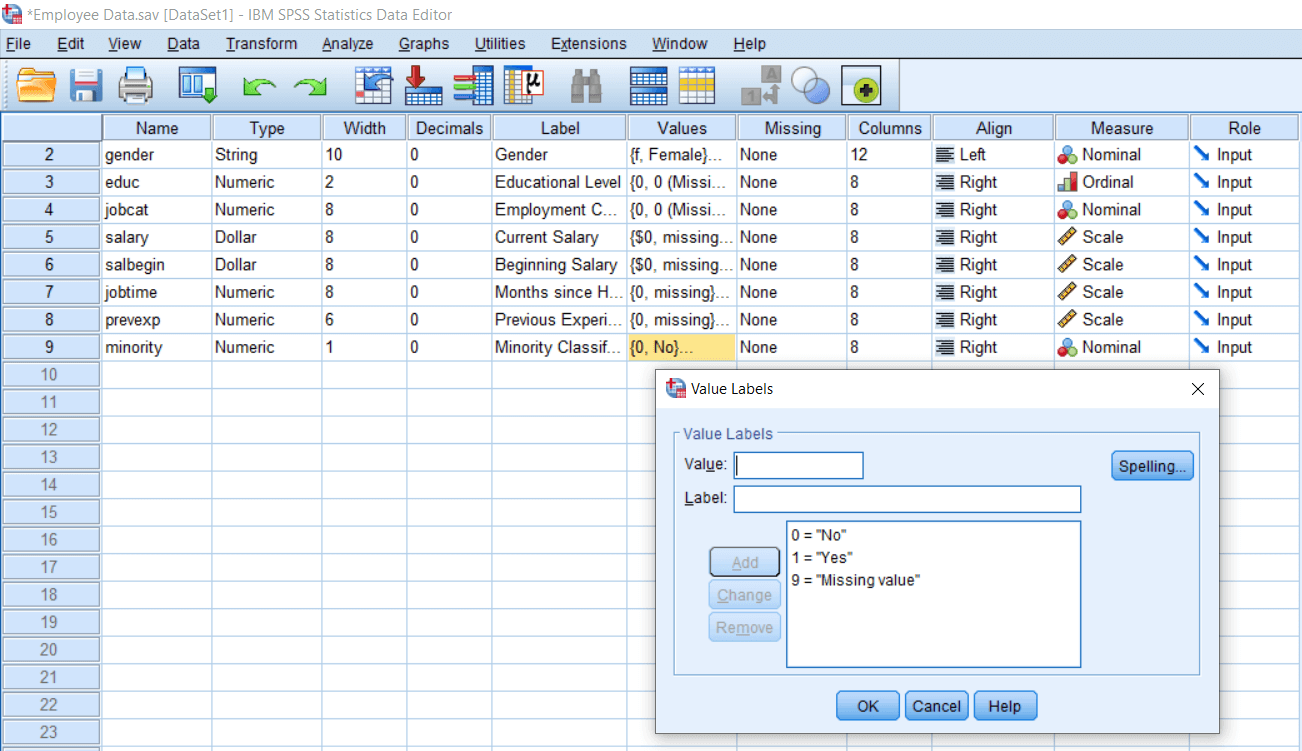
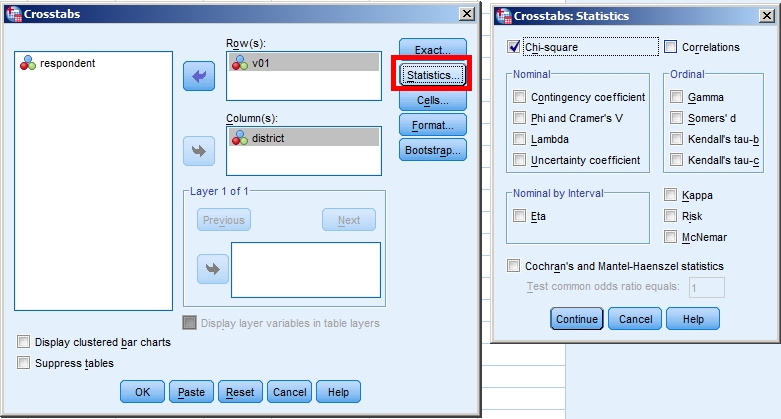
This tutorial will show you how to use SPSS version 12.0 to performīinomial tests, Chi-squared test with one variable, andĬhi-squared test of independence of categorical variables on nominally The result of square will be divided by the expected frequency.Using SPSS for Nominal Data (Binomial and Chi-Squared Tests) We deduct expected from the observed, and we square it. So when we calculate the chi-square, we take the observed frequencies and the expected frequencies. In the denominator, we again have the expected frequency. The formula of chi-square test is used for the calculation. The chi-square test is nothing but a test of the difference between observed and expected frequencies.

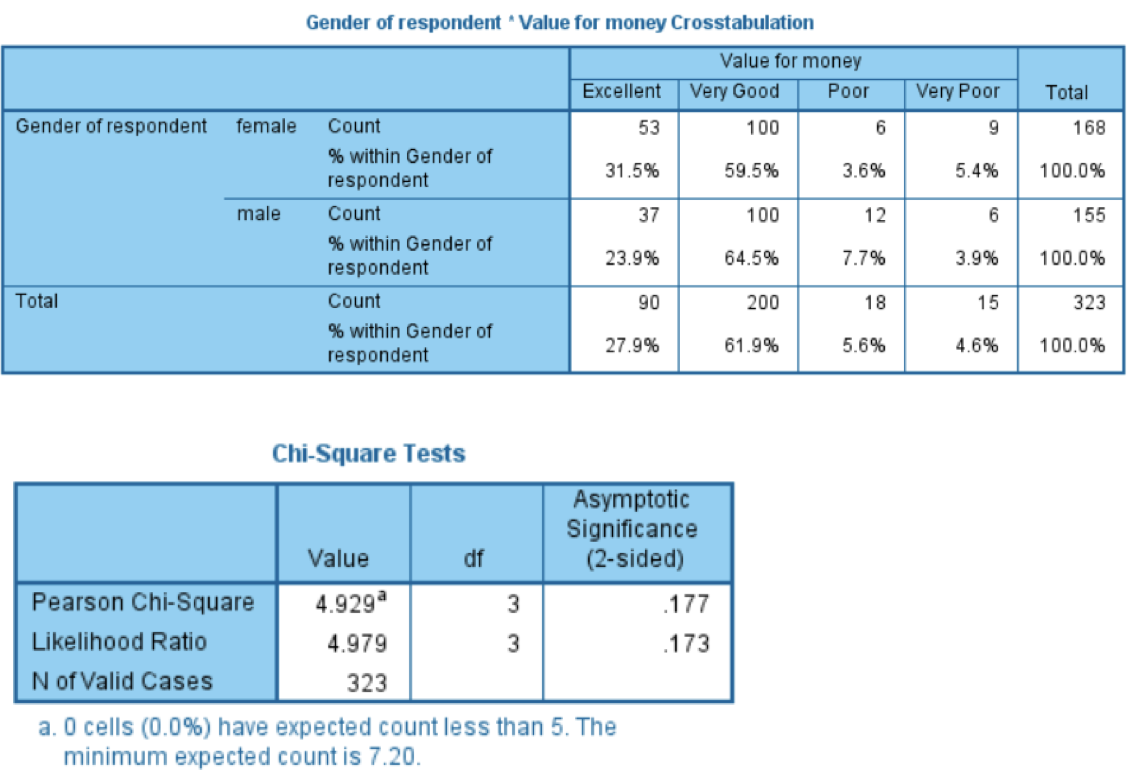
If we divide 100 by 4, we will get 25 each for the expected frequency for males and females. In our case, the number of categories is 4. Expected frequencies can be derived by finding out the total number of observations and dividing it by the number of categories. So observed frequencies and expected frequencies both are d ifferent from each other. That means 25 male subjects and 25 females are favoring each of the four football teams. If we have 100 subjects in the male category and 100 subjects in the female category, we expect 25 subjects in each of the four cells. In the table, we have recreated expected frequencies as well. So the table can be redrawn in such a way that we can show expected and observed frequencies. So these actual observations are different, but we expect them to be similar across all the categories. That means 20 male football fans in favor of each team, and similarly for the females. So if we are having a total of 100 males and 4 teams, we expect that there would be 20 male subjects per team. The expectation is that there must be an equal number of voters for each football team. When a researcher conducted research, these are the actual individual who voted in favor of different teams. So these are the actual observed frequencies. In fact, if there are atleast five frequencies or observations in each expected cell, then we consider our data sufficient for chi-square testing. The second important assumption of chi-square is that the expected cell frequencies should not be too small. So the first assumption of the Chi-square test is that individual observations are independent of each other. The selection of the 30 males in the first category does not affect selecting these 20 males in the second category and so on. Now the observation 30 males for Germany and 29 males for France, they must be independent of each other. In the female category, 40 females voted for Germany, 15 for France, 18 for Italy and 27 for Brazil. We can see 30 males voted for Germany, 20 for France, 15 for Italy and 35 for Brazil. He will ask them which is their most favorite team. The researcher has randomly taken 100 male football fans and 100 female football fans. This table is basically about measuring the popularity of football game between males and females. Now, look at the values written in each cell of this table. So this is the table that we have created for the demonstration purpose. Suppose we get the data in the format of frequencies, and we categorize our data in the format of a contingency table. The first one is individual observation should be independent of each other. In SPSS, there are two major assumptions of the Pearson chi-square test. In this section, we are going to learn the Assumptions of Chi-square test. Next → ← prev Assumptions of Chi-Square test


 0 kommentar(er)
0 kommentar(er)
